基于遗传算法的课程表问题求解方法的研究
来源:wenku163.com 资料编号:WK1632520 资料等级:★★★★★ %E8%B5%84%E6%96%99%E7%BC%96%E5%8F%B7%EF%BC%9AWK1632520
资料介绍
摘 要
大学课程表属于NP问题,人们尝试过用很多方法解决,最终找到利用模拟生物界自然选择和自然遗传机制的遗传算法能够搜索到我们想要的最优解。
对于解决排课问题,首要的是对现实情况的分析和建立起合理的数学模型。课程表存在着普遍的五个要素,班级、教师、教室、时间和课程。根据分析的结果,我们把教师与课程等同,班级与教室等同后,转化为三要素,这大大简化了我们对染色体编码的复杂程度(染色体的编码直接影响到交叉算子)接下来随机产生初始种群,然后根据所要搜索的结果,设定适应度函数。适应度函数的选取直接影响到,每一代的优良程度,进而更加影响到最后的结果。
有了初始种群和适应度函数,就接触到了遗传算法最关键的所在,遗传操作。选择、交叉和变异算子将作用于每一代种群的个体。这里,在进行交叉操作很变异操作的时候,交叉概率和变异概率的选取很大程度上影响算法的收敛速度和近优解的质量,所以,需要提出一个自适应的概念,使最优个体和较优个体不参加和少参加交叉和变异,即个体的交叉概率和变异概率根据个体的适应度在平均适应度和最大适应度之间进行线性调整。为了利于实现计算,产生一个参数K,直接进行自适应调整。
关键词:遗传算法,编码,染色体,初始种群,适应度函数,遗传操作,自适应
Application of the Adaptive Genetic Algorithm in Timetable Problem
Abstract
In recent years, genetic algorithms are developed a new algorithm to optimize, it is based on the biological mechanism of natural selection and heredity to achieve all of the individual adaptability, making use of colony searching technology, and is particularly applicable for the resolution of complicated non-linear problems intractable with traditional searching methods. Timetable problem is a multi-factor optimized decision problem and is typical problem in. constitution and planning. It has been proved as a kind of NP-problem. According to the character of courses assignment in an university, a kind of codes and fitness function are designed and solved by Genetic Algorithm, and a kind of crossover and mutation algorithm is used Genetic operation. With adaptive crossover and mutation probability employed, Final the example verifies that genetic algorithm is value of the effectiveness and feasibility.
Key words: Genetic Algorithms, timetable problem, codes,crossover operator; Adaptive
研究方法
由于排课问题的多因素、多约束条件的限制,以及需要人性化处理排课时间的要求。对于这种复杂的系统优化问题,从多方面考虑,使用遗传算法解决问题,理论上讲是较为有效的。虽然说,遗传算法还有诸多不足,但在寻找最优和靠近最优解的问题的处理上,还有有相当优势的。
排课系统开发采取的是MATLAB软件。MATLAB当中拥有遗传算法工具箱函数,对遗传算法程序的编写大大降低了其复杂性,还有,由于MATLAB高级语言的通用性,对问题用M文件编码,与此配对的是MATLAB先进数据分析、可视化工具、特殊目的的领域工具箱和展现给使用者具有研究遗传算法可能性的一致环境。
课题难点
本课题采用的是遗传算法解决排课问题,重点在于找到一种最优的算法或者是接近于最优的算法,在一代又一代的遗传中产生最优解,而从初试种群到最后一代,我们需要得这些解进行系统、科学合理的编码。最终,在计算机上运行,运行就需要一个时间遗传一代的时间,关键出在了编码的问题上。如果编码过于简单,很难找到最优解,可能由于种群的单一性,导致了过早的收敛,无法产生最优;但如果编码过于复杂,运算复杂,遗传速度缓慢,我们最后也找不到最终需要的答案。
所以,编码在遗传算法就成了关键的难点所在。解决这一问题,变成了本课题的难点所在。
关键问题
上面编码最了简单的分析,已经找出了问题的难点所在。而问题的关键,我认为在初始种群的选取和交叉算子。
初始种群的选取,在很大程度上决定了以后每代当中优良基因的遗传。如果初始种群选取的不合理、没有代表性,最终遗传算法根本无法搜索到我们需要的优良基因。
交叉算子则决定了物种遗传,如果没有交叉,就不可能产生新物种;反之,则会丧失优良基因。
所以,在我看来,问题的关键所在就是要处理好初始种群和交叉算子。
可行性
根据多方面的资料和论文显示,利用遗传算法解决学生排课问题还是相当可取的。
大学课程确实有其复杂行,但是遗传算法在处理多问题优化的问题上,有很多行之有效的解决办法,和解决该问题的工具(函数)。在遗传算法的领域里,排课还不算是太过复杂的系统,可行性是不言而喻的。
目 录 14000字
任务书 I
摘 要 II
ABSTRACT III
第1章 绪 论 6
第2章 遗传算法 3
2.1 遗传算法简介 3
2.1.1 遗传算法的优点 3
2.1.2 遗传算法的不足之处 4
2.2 遗传算法的基本知识 4
2.2.1 遗传算法的基本术语 4
2.2.2 遗传算法的运算流程 5
2.3 自适应遗传算法简介 5
2.4 自适应遗传算法计算流程 6
第3章 排课问题的现实分析和数学模型 6
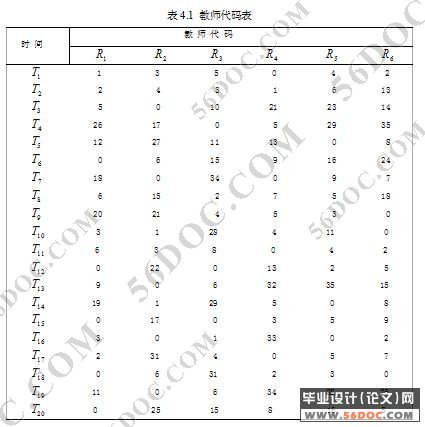
第4章 编码策略 8
4.1编码 8
4.1.1编码方法 8
4.1.2编码评估 8
4.2 染色体 9
4.3 具体编码方法 10
第5章 可行初始种群的产生 11
5.1初始群体的产生 12
5.2 排课问题可行解的产生 12
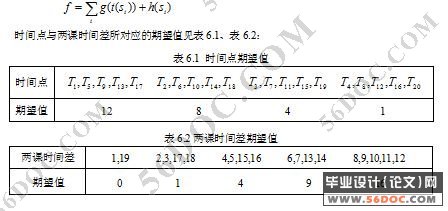
第6章 适应度函数 12
6.1适应度函数 13
6.2适应度函数设计满足的条件 13
6.3适应度函数的具体设计 13
第7章 遗传算子 15
7.1 选择(Selected)操作 15
7.2 交叉(Crossover)操作 15
7.3 变异(Mutation)操作 18
7.4 自适应调整概率 19
7.5 最优保存策略 19
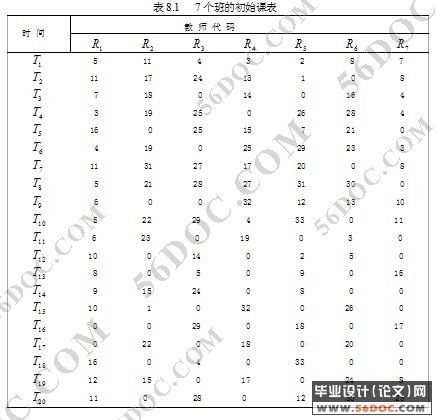
第8章 结果分析 21
8.1 数值实例 21
8.2 结果分析 25
第9章 结 论 26
参考文献 27
致 谢 28
|







