中文摘要
小波变换发展到现在在许多不同的研究领域都取得了令人瞩目的研究成果,尤其是在信号分析和图象处理方面,小波变换更显示出其无法比拟的优越性。与经典的傅立叶分析理论相比,小波分析算是近年来出现一种新的数学分析方法。它被数学家和工程师们独立地发现,被看作是多元调和分析50年来发展的一个突破性的进展。它反映了大科学时代学科之间相互渗透、交叉、融合的趋势,是纯粹数学与应用数学及工程技术殊途同归的典范。
它采用改变时间—频率窗口形状的方法很好地解决了时间分辨率和频率分辨率的矛盾,在时间域和频率域内都具有很好的局部化性质。对信号中的低频成分,采用宽时间窗,得到低的频率分辨率;对信号中的高频成分,采用窄的时间窗,得到高的频率分辨率。小波变换的这种自适应性,使它在工程技术和信号处理方获得广法的应用。小波理论是近十几年发展起来的新的信号处理技术,因其在时间域和频率域都可以达到高的分辨率,被称为“数学显微镜”。
小波分析如今已经广泛地应用于信号处理、图象处理、量子理论、地震勘测、语音识别与合成、雷达、CT成像、机器视觉等科技领域。
本文首先介绍了小波变换的基本理论知识,然后通过一系列的实例,包括与其他分析方法,如傅立叶分析方法等进行比较,说明小波变换在信号分析和图象处理中的应用。
关键词:小波变换,傅立叶变换,小波图象处理
WAVELET WITH APPLICATION RESEARCH IN
SIGNAL AND IMAGE PROCESSING
Abstract
The field of Wavelet Transform and its applications in signal and image processing has been proved to be an amazing one.Compare with the theory of classics Fourier analysis, the wavelet analysis appears to be one new mathematical analysis method in the recent years. It is independently discovered by the mathematician and engineers, which is regarded as an unprecedented progress of the multi-harmonic analysis for the 50 years development. It had reflected the seeping, overlapping, and the fusion tendency of discipline mutually in the greatly scientific time. And it is the apotheosis of the pure mathematics, the applied mathematics and the project technology reach the same goal or conclusion from different approaches.
It adopts the method of time - Frequency window to solve the contradiction of time and frequency resolution ratio well, which has very good localization properties in the time and frequency intra-areas. TO the low frequency components of signals, use wide time window with low-frequency resolution. To the high frequency components of signals, use a narrow time window, with high-frequency resolution. The adaptability of wavelet transform makes it broad applied in the engineering technology and signal processing side. Wavelet theory develops new signal processing technology in almost 10 years, which can achieve high resolution in time and frequency domain, known as the "mathematical microscopes".
The wavelet analysis already has been widely applied to technical domain and so on signal processing, imagery processing, quantum theory, seismic survey, speech recognition and synthesis, radar, CT imagery, machine vision.
This project aims to introduce the basic theory of wavelet tranform and demostrate a serial of its applications, including breakpoint dection, noise elimination, multiresolution and data compression. From these cases we can derive the advantages of wavelet transform easily compared with other transform, such as Fourier Transform (FFT), and so on. (毕业设计网 )
Key words: wavelet transform, Fourier transform, wavelet photo processing
绪论
小波变换发展到现在在许多不同的研究领域都取得了令人瞩目的研究成果,尤其是在信号分析和图象处理方面,小波变换更显示出其无法比拟的优越性。
与经典的傅立叶分析理论相比,小波分析算是近年来出现一种新的数学分析方法[1]。它被数学家和工程师们独立地发现,被看作是多元调和分析50年来发展的一个突破性的进展,它反映了大科学时代学科之间相互渗透、交叉、融合的趋势,是纯粹数学与应用数学及工程技术殊途同归的典范。
小波分析属于时频分析的一种,它在时间域和频率域同时具有良好的局部化性质,是一种信号的时间—尺度(时间—频率)分析方法,具有多分辨率分析的特点,而且在时频两域都具有表征信号局部特征的能力,被誉为分析信号的显微镜[2]。小波分析如今已经广泛地应用于信号处理、图象处理、量子理论、地震勘测、语音识别与合成、雷达、CT成像、机器视觉等科技领域。
任何一个理论的发现和提出都有一个漫长的准备过程,小波分析也不例外。1910年Harr提出了小波规范正交基,这是最早的小波基[2],当时并没有出现“小波”这个词。1936年Littlewood和Paley对Fourier级数建立了二进制频率分量理论:对频率按2j进行划分,其Fourier变换的相位变化并不影响函数的大小,这是多尺度分析思想的最早来源。1946年Gabor提出了加窗Fourier变换(或称为短时Fourier变换)对弥补Fourier变换的不足起到了一定的作用,但是并没有彻底解决问题。后来,Calderon、Zygmund、Stern和Weiss等人将L-P理论推广到高维,并建立了奇异积分算子理论。1965年,Calderon给出了再生公式。1974年,Coifmann对一维空间HP和高维HP空间给出了原子分解。1975年,Calderon用他早先提出的再生公式给出了抛物形HP的原子分解,这一公式现已成为许多函数分解的出发点,它的离散形式已经接近小波展开。此后,许多数学家为着各种不同的目的,给出了各类函数空间上的“原子分解”、“分子分解”、“拟正交分解”、“弱正交分解”、“框架分解”等。1976年,Peetre在用L-P方法给出Besov空间统一描述的同时,引入Besov空间的一组基,其展开系数的大小刻画了Besov本身。1981年,Stromberg通过对Harr正交基的改进,引入了Sobolev空间的HS正交基,这些工作为小波分析奠定了基础。



目录
第1章 绪论 1
第2章 理论分析 5
2.1时—频局部化分析和连续小波变换 5
2.1.1短时傅立叶变换(STFT) 5
2.1.2连续小波变换(CWT) 6
2.1.3连续小波变换的离散化(DWT) 8
2.2 多分辨率析 8
2.2.1函数空间的剖分 8
2.2.2理想滤波器组 9
2.3离散小波变换的快速算法(FWT)—Mallat算法 10
2.4提升小波变换 12
第3章 一维小波分析应用 14
3.1分别用FFT、STFT和DWT分析信号 14
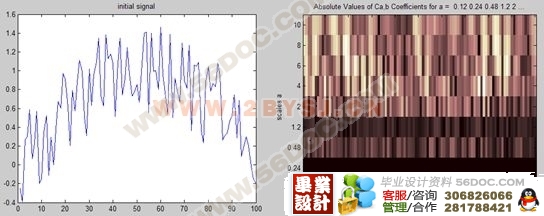
3.2连续小波变换(CWT) 14
3.3一维小波分析对信号进行单尺度和多尺度分解 15
3.4一维小波分析信号奇异点检测 16
3.5一维小波分析对信号进行消噪处理 17
(毕业设计网 )
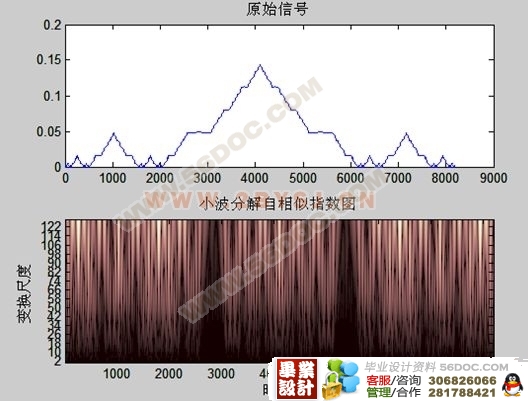
3.6一维小波分析自相似性检测 18
3.7一维小波分析信号压缩 19
第4章 二维小波分析应用 21
4.1二维小波分析图象消噪 21
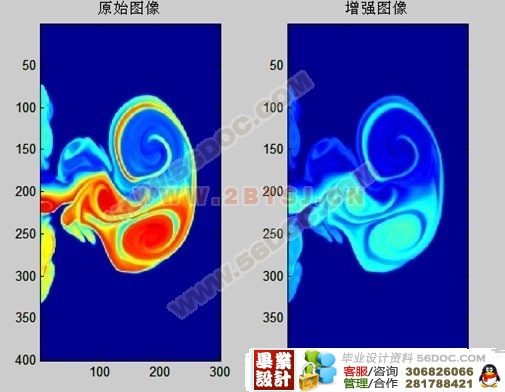
4.2二维小波分析图象增强 21
4.3二维小波分析图象融合 22
4.4二维小波分析图象压缩 23
4.5二维小波分析图象边缘提取 24
4.6小波变换和DCT变换的比较 25
结论 28
致谢 29
参考文献 30
附录 31
附录一 一维小波分析函数 31
附录二 二维小波分析函数 32
附录三 其他 33
附录四 实验程序 34 |

